以下、符号なし16 bit整数の除算を例に、除算のアルゴリズムを改めて解説いたします。符号付整数どうしを割る場合には、除数と被除数の双方を絶対値に変換して除算を行い、除算結果にあらためて符号をつけます。このとき、商につける符号は除数の符号と被除数の符号の排他論理和、余りにつける符号は被除数の符号となります。
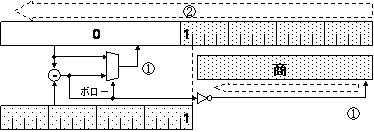
除算は、被除数から除数がいくつ引けるかを求めればよいのですが、一つずつ減算するのは非効率的です。そこで、除数をk bit左シフトしたものを被除数から引くことを試み、引けた場合には商のbit kを立てることを繰り返すことといたします。これをおこなう論理のフローチャートを下図に示します。

一つの疑問は、除数を何ビット左シフトしたところから計算を始めればよいか、という点です。この答えは、それを差し引くことによって除数の上位ビットをゼロにするに充分な数だけ左シフトすればよい、ということになります。
16ビット符号なし整数どうしの除算の場合、除数の最小値は1であり、被除数の最上位ビット(bit 15)が立っている可能性があります。そこで、最初の引き算の試みは、除数を15 bit左シフトしたものを被除数から差し引くこととなります。被除数を格納するレジスタは、除数のビットと対応するよう、上位を15 bit拡張して拡張部分に0を格納しておきます。
ここで、除数が被除数よりも小さい場合は、これを差し引いて新たな被除数とし、商の最上位ビットに1を立てます(実際には、商はシフトレジスタにおき、最下位から1をシフトインします)。除数が被除数よりも小さい場合は差し引かずに商の最上位ビットを0とします。
これを、被除数を左シフトさせながら16回繰り返すことで、最後には被除数の部分に余りが残り、16 bitの除算が完了します。
この考えに基づく除算論理を、この文書の以前の除算の解説には記載していました。この論理は正しい結果を与えるのですが、必ずしも効率的な構成であるとはいえません。引き算を行い、その結果により差か元の数値かを選択するという論理構成とした場合、引き算と選択という二つの操作を順次実行することになり、論理ユニット二つ分の遅延が発生いたします。
これを改善するには、さしあたり引き算をおこなうこととして、商にはアンダーフロービットを反転したもの(つまり引ければ1、引けなければ0)をセットしておきます。そして、次の桁の計算をする際に、引けない場合はすでにおこなってしまった引き算の効果を打ち消す演算を追加しておこなえばよいということになります。
引き算の効果を打ち消す演算とは、除数を加算する演算ということになるのですが、次の桁の演算時には被除数は1ビット左シフトされておりますので、除数の2倍を加算することですでにおこなわれた減算の効果を打ち消すことができます。そして、その桁の除算は除数を減算することによりおこなわれるわけですから、前の桁で引けなかったときの演算は、2倍加算して1倍を減算する、すなわち除数を加算すればよいことになります。
つまりは、前の桁で引けた場合は次の桁の演算は除数を減算し、前の桁で引けなかった場合は次の桁で除数を加算するという操作を続けていけばよいというわけです。
FPGAの加減算機能として、制御線によりダイナミックに加算と減算を切り替えることができるものもあります。このような場合には、加減算切り替えに要する追加の論理資源はゼロであり、セレクタが不要になった分だけ論理資源も節約できるし、遅延時間も少なくなると期待されます。
このアルゴリズムの欠点は、余りが負になることがある点ですが、余りが負になったことは商の最下位がゼロであることから検出できますし、負の余りには除数を加算することで正しい余りを得ることができます。これは、結果の後始末の部分でおこなえばよいでしょう。
以下に示すソースコードは、符号なし16 bit整数どうしの除算モジュールです。入力ポートのnumerator_pには被除数(分子)、denominator_pに除数(分母)を接続いたしますと、出力ポートのquotient_pに商が、surplus_pに余りが出力されます。
遅れを評価するため、トップモジュール“div_u16_nl”はクロック信号(clock)に同期して、入力信号を一旦レジスタに格納してその出力を除算モジュール“unsigned_div16”に送り、モジュールの出力も一旦レジスタに受けた後にポートから出力するようにしています。
// followings are sample codes of "Verilog HDL Code Book"
// Test for "Cyclone III EP3C25F324C6"
module div_u16_nl(
input [15:0] numerator_p,
input [15:0] denominator_p,
output reg [15:0] surplus_p,
output reg [15:0] quotient_p,
input clock);
reg [15:0] num, den;
wire [15:0] s, q;
unsigned_div16 u1 (.num(num), .den(den), .s(s), .q(q));
always @(posedge clock) begin
num <= numerator_p;
den <= denominator_p;
surplus_p <= s;
quotient_p <= q;
end
endmodule
module unsigned_div1(
input [32:0] num1,
input [15:0] den1,
output [32:0] s1,
output q1);
assign s1 = num1[32] ? {num1[31:0], 1'b0} + {1'b0, den1, 16'b0}
: {num1[31:0], 1'b0} - {1'b0, den1, 16'b0};
assign q1 = ~s1[32];
endmodule
module unsigned_div2(
input [32:0] num2,
input [15:0] den2,
output [32:0] s2,
output [1:0] q2);
wire [32:0] work;
unsigned_div1 u1(.num1(num2), .den1(den2), .s1(work), .q1(q2[1]));
unsigned_div1 u2(.num1(work), .den1(den2), .s1(s2), .q1(q2[0]));
endmodule
module unsigned_div4(
input [32:0] num4,
input [15:0] den4,
output [32:0] s4,
output [3:0] q4);
wire [32:0] work;
unsigned_div2 u1(.num2(num4), .den2(den4), .s2(work), .q2(q4[3:2]));
unsigned_div2 u2(.num2(work), .den2(den4), .s2(s4), .q2(q4[1:0]));
endmodule
module unsigned_div8(
input [32:0] num8,
input [15:0] den8,
output [32:0] s8,
output [7:0] q8);
wire [32:0] work;
unsigned_div4 u1(.num4(num8), .den4(den8), .s4(work), .q4(q8[7:4]));
unsigned_div4 u2(.num4(work), .den4(den8), .s4(s8), .q4(q8[3:0]));
endmodule
module unsigned_div16(
input [15:0] num,
input [15:0] den,
output [15:0] s,
output [15:0] q);
wire [32:0] work1, work2;
assign s = q[0] ? work2[31:16] : work2[31:16] + den;
unsigned_div8 u1(.num8({17'h0, num}), .den8(den), .s8(work1), .q8(q[15:8]));
unsigned_div8 u2(.num8(work1), .den8(den), .s8(work2), .q8(q[7:0]));
endmodule
RTLチャートをみていきましょう。まず、トップモジュールは次のようになります。
16ビット除算モジュールの内部を以下に示します。
16ビット除算モジュールは8桁の除算を行うモジュール二つから構成されています。結果の最下位が0の場合、本来引いてはならない除数が引かれて余りが負となっていますので、余りに除数を加算する処理をおこなっています。
8桁の除算モジュールは4桁の除算モジュール二つ、4桁の除算モジュールは2桁の除算モジュール二つ、2桁の除算モジュールは1桁の除算モジュール二つから構成されます。これらの内部構成は商のビット幅が異なるだけでほとんど同じですので、上には4桁の除算モジュールを代表として示しておきました。
1桁の除算モジュールは以下のようになっています。
左側に加算器が二つ並んでいますが、上側の加算器は一方の入力を負論理とし、1を加算することで減算器として動作します。図の右側はセレクターで、加算結果と減算結果のいずれかを出力します。加減算に関係しない部分は、入力信号をそのまま出力しています。
今回ご紹介した除算アルゴリズムは、セレクタを省略するアルゴリズムを意図したのですが、加算器と減算器を別々に配置し、この結果をセレクタで選択する形の論理が合成されています。このような形になりますと、改良前の論理と同じようにセレクタでの遅延時間が含まれ、更には改良前の論理に比べて加算器が余分に必要になってしまいます。
おそらく、加減算をダイナミックに切り替えできる論理エレメントをもつデバイスを対象とするのであれば、今回ご紹介したアルゴリズムは速度の点でも、資源の点でも改善されるものと思われますが、今回取り上げましたCycloneIIの場合には改善効果は認められませんでした。
この論理をAltera社製のFPGA“Cyclone III EP3C25F324C6”に配置した場合の資源の消費量を、前回ご紹介した改良前の結果と比較したのが下表です。
| アルゴリズム | 最大クロック周波数 | ロジックエレメント |
| 改良前(前回) | 21.16 MHz | 543 |
| 改良後(今回) | 20.99 MHz | 565 |
原理的には改善が見込まれるアルゴリズムですが、デバイスによってはかえって特性が悪化することもあるという結果となりました。当初は本文書の他の除算アルゴリズムも書き換える予定でしたが、上の結果を見る限り、いずれが優れているかは必ずしも明確でなく、他の文書につきましては今回おこないました改良を加えないことにしました。
今回の改良を施すための変更点は、最下位のモジュールを、減算結果と元の値を切り替えていたことから、加算減算の切り替えに変更したことと、被除数を格納するレジスタの幅を1 bit拡大したことです。後者は、被除数として負の値を取り扱う必要が生じることから、符号ビットを拡張したものです。
この論理の動作を、Qualtus II付属のシミュレータでテストした結果を下図に示します。
クロック信号clockの立ち上がりに同期して、入力ポートの信号がレジスタnumとdenに取り込まれ、次のクロック信号の立ち上がりに同期して演算結果が出力レジスタに取り込まれます。シミュレーションは入力データの小さい側と大きい側でいくつかおこなっていますが、いずれも正常な結果が得られています。
なお、ゼロで割る演算は原理的に許されておらず、本来は除数のゼロを検出してエラーとする処理が必要ですが、このモジュールにはそのような機能を設けておりません。このため、除数としてゼロが与えられると、商は最大値となり、余りは被除数となります。これは商が最大値にクリッピングされているのと同じ結果であり、使用目的によっては特別なエラー処理をせずに使用可能です。